
You then use the intersections to compose the shot. If you use those numbers to create squares with those widths, you can pretty much create a Golden Spiral:

The first few numbers in the sequence are 0, 1, 1, 2, 3, 5, 8, 13, 21, 34. The Fibonacci Sequence is pretty simple to understand: you start with zero and 1, then get the next number by adding up the two numbers before it. If you start in the bottom left and make an arch to connect the far side of each square-and-small-rectangle cross section, you’ll get the Golden Spiral. You can also make a new Golden Rectangle out of the smaller rectangle, like this one I’ve outlined in blue:Ī traditional Golden Ratio diagram has eight Golden Rectangles:Īnd here’s the smallest Golden Rectangle, #8: Together, they create a complete Golden Ratio layout and a base for the Golden Spiral. By sectioning off that square, you automatically create another, smaller rectangle (outlined in green). The red square has four sides equal in length, and that length is equal to the shortest length of the rectangle. Ignore the black lines and look at the red and green boxes: When you place a square inside the rectangle, it creates another, smaller rectangle.
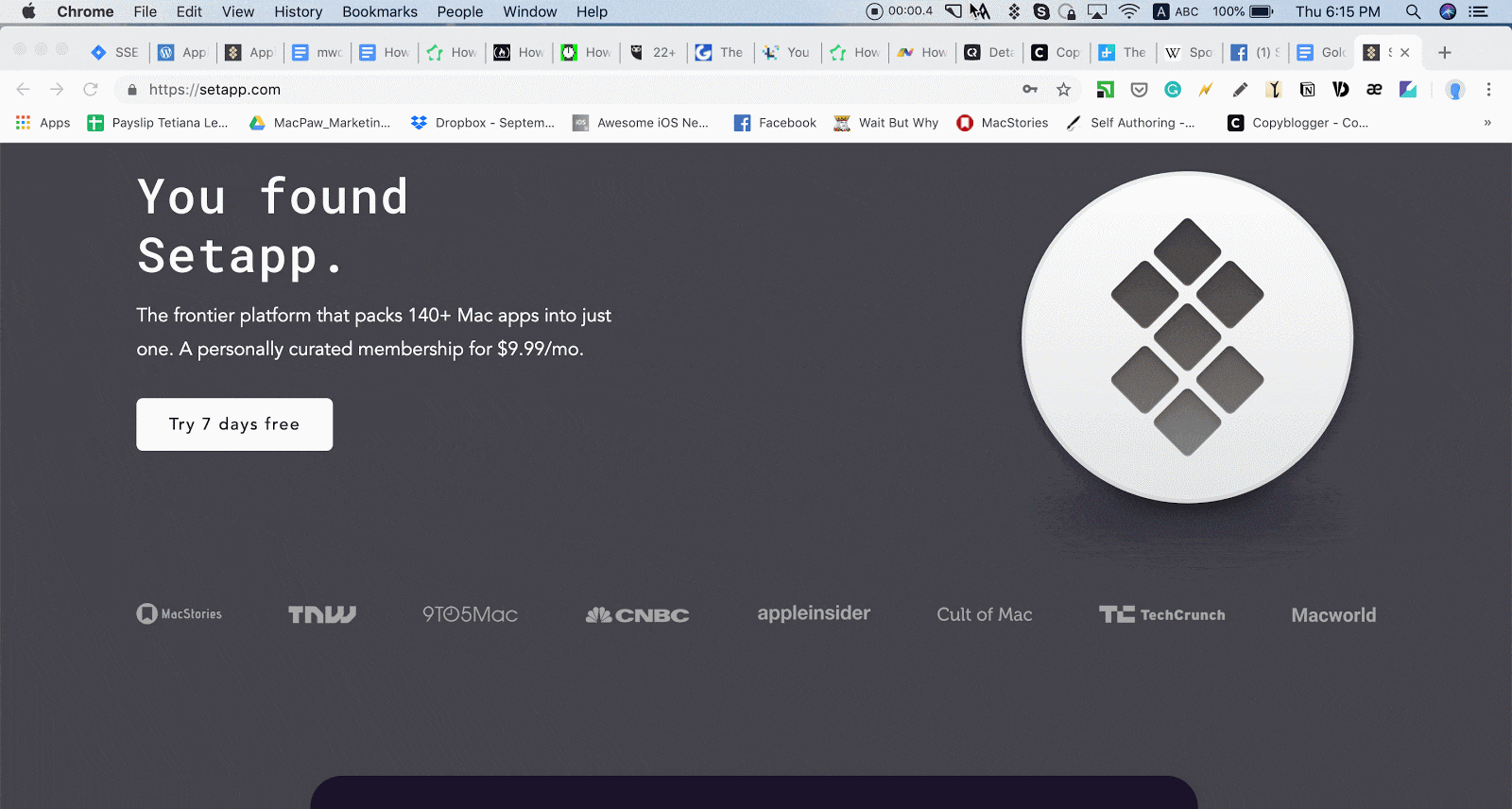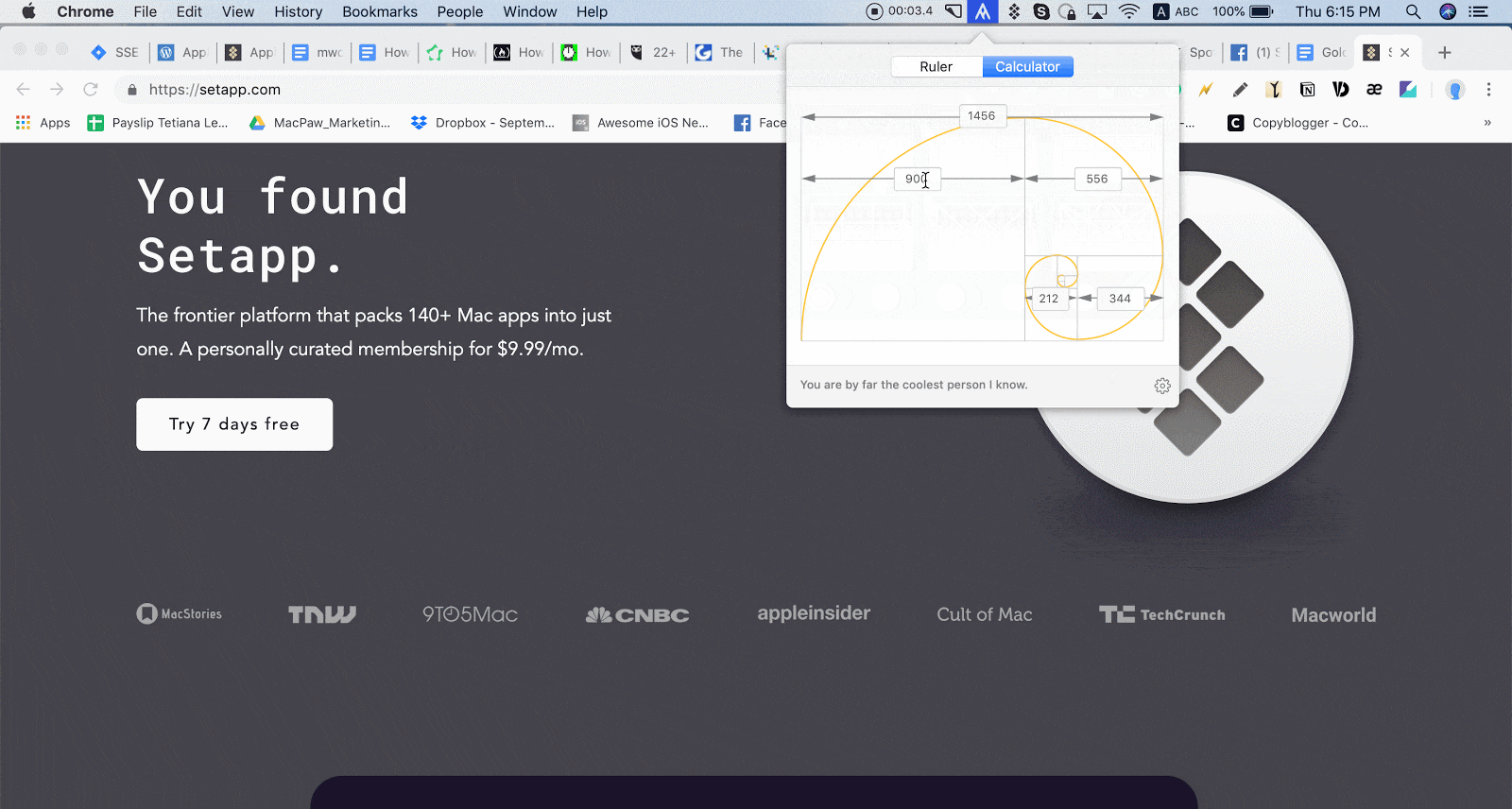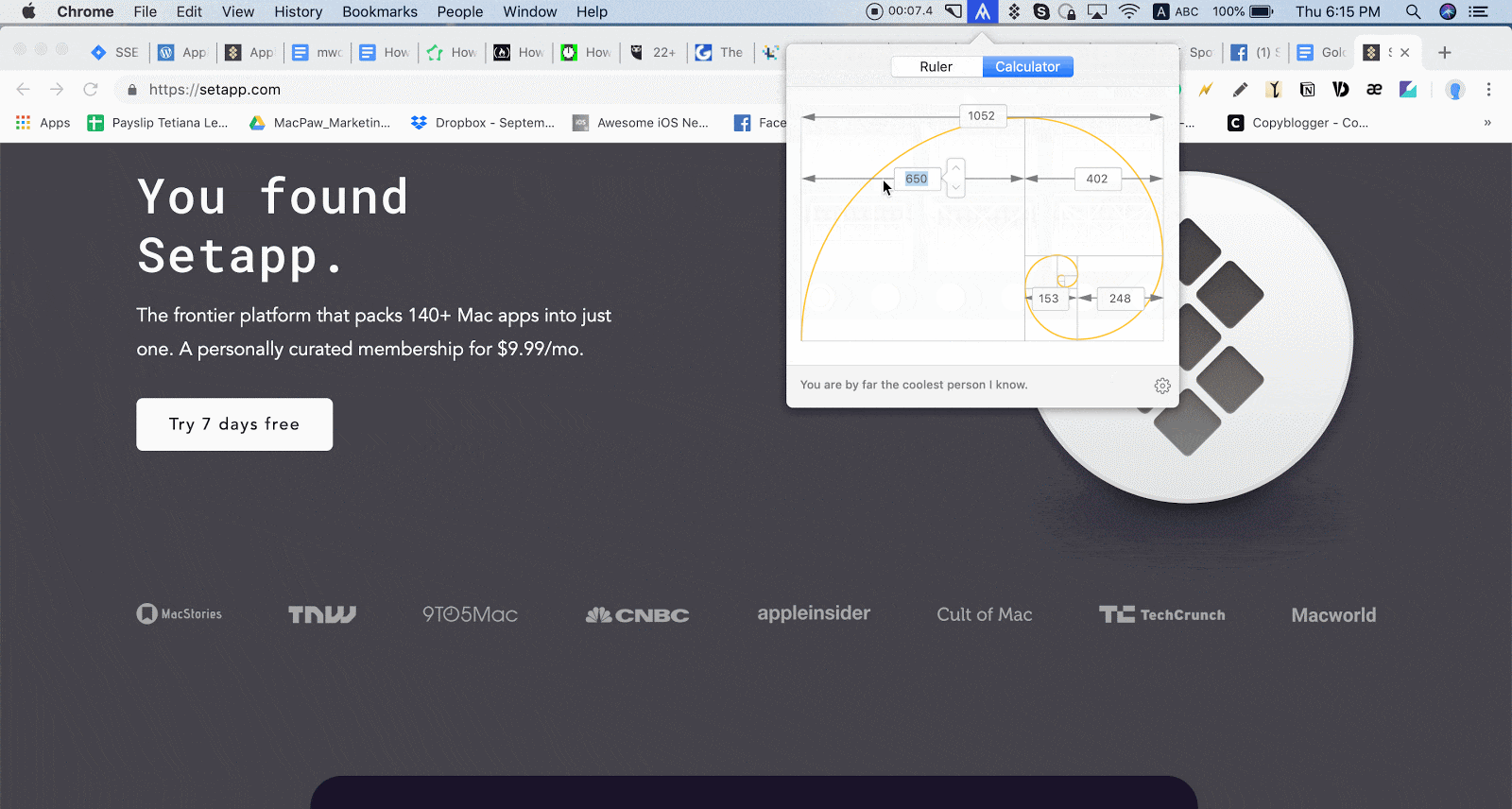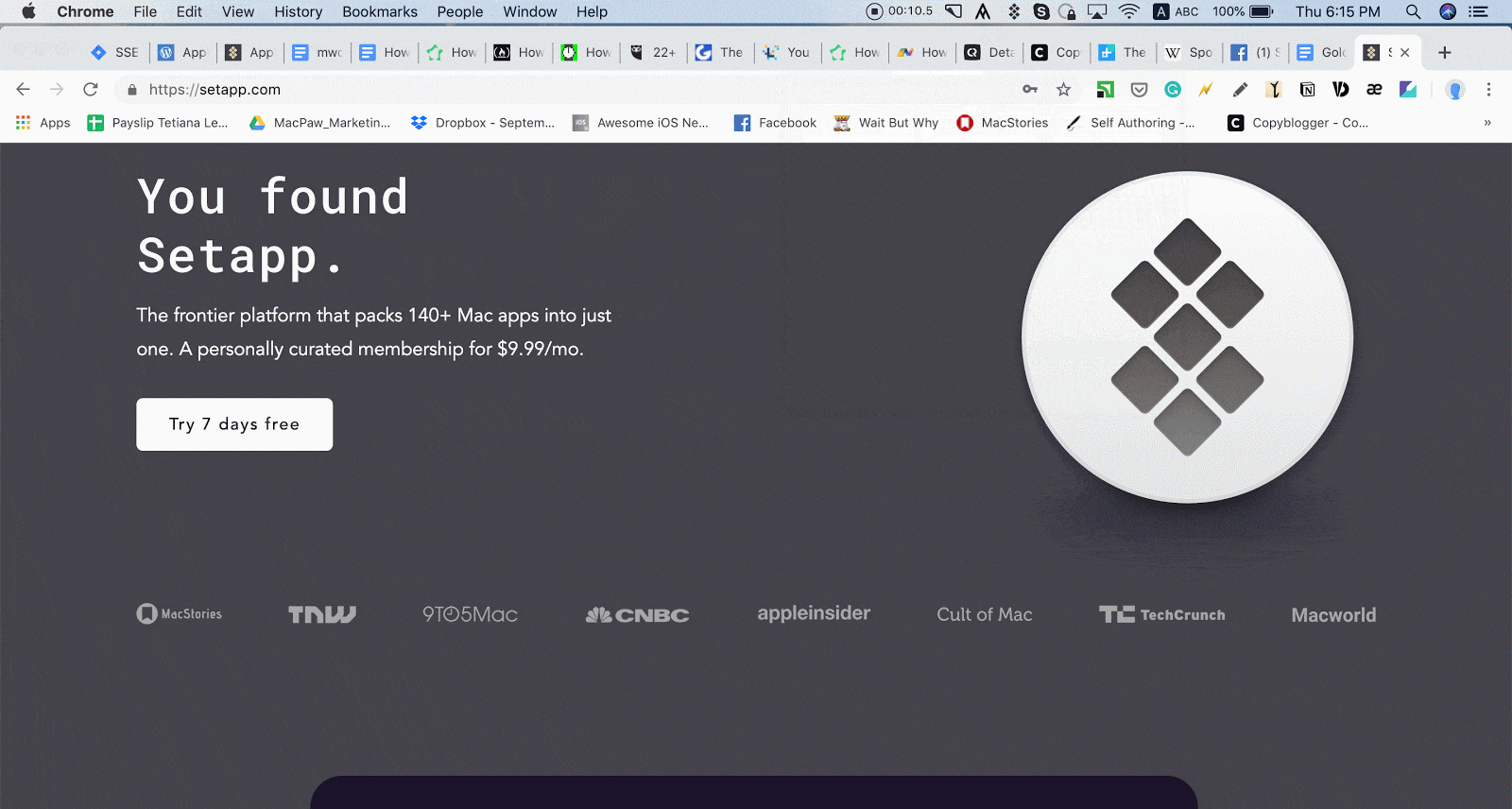
Back to the Golden Rectangle, because it’s so much easier to understand So, (a + b) divided by (a) equals 1.618, and (a) divided by (b) also equals 1.618. The entire length (a + b) divided by (a) is equal to (a) divided by (b). You take a line and divide it into two parts – a long part (a) and a short part (b). The Golden Ratio is a number that’s (kind of) equal to 1.618, just like pi is approximately equal to 3.14, but not exactly.


 0 kommentar(er)
0 kommentar(er)
